What is the Associative Property of Multiplication?

What is the Associative Property of Multiplication? Welcome to an in-depth exploration of the Associative Property of Multiplication. This fundamental concept in mathematics lays the foundation for understanding how numbers interact with one another when we multiply.
In this comprehensive blog post, we will break down the associative property, explain its importance, provide real-life examples, and offer tips for mastering this concept. So, let’s dive right in!

What is the Associative Property of Multiplication?
The Associative Property of Multiplication is one of the essential properties of multiplication that describes how numbers can be grouped when you’re multiplying them together. It states that the grouping of numbers in a multiplication equation doesn’t affect the final product.
In simpler terms, you can change the order in which you multiply a set of numbers, or you can group them differently using parentheses, and the result will remain the same.
Mathematically, the associative property can be expressed as:
(a * b) * c = a * (b * c)
Where:
- (a * b) * c represents the multiplication of a and b first, and then multiplying the result by c.
- a * (b * c) represents multiplying b and c first, and then multiplying the result by a.
What is the Associative Property of Multiplication
Why is it Important?
Understanding the associative property is crucial because it allows us to simplify complex multiplication problems and work with numbers more efficiently. It provides a basis for mental calculations, and it’s often used in algebra and higher-level mathematics.
Real-life Examples
Let’s explore a few real-life scenarios to illustrate the significance of the associative property:
- Sharing Treats: Imagine you have 3 friends, and you want to share 4 packs of candies equally among them. You can either distribute the candies in groups of 2 first and then distribute the remaining 2, or you can distribute 1 pack to each friend first and then distribute the remaining pack. In both cases, everyone gets the same number of candies, thanks to the associative property.
- Baking Cookies: When you’re following a recipe and need to double it, you can either double each ingredient individually or double the entire recipe. The associative property allows you to choose the most convenient approach without changing the final outcome.
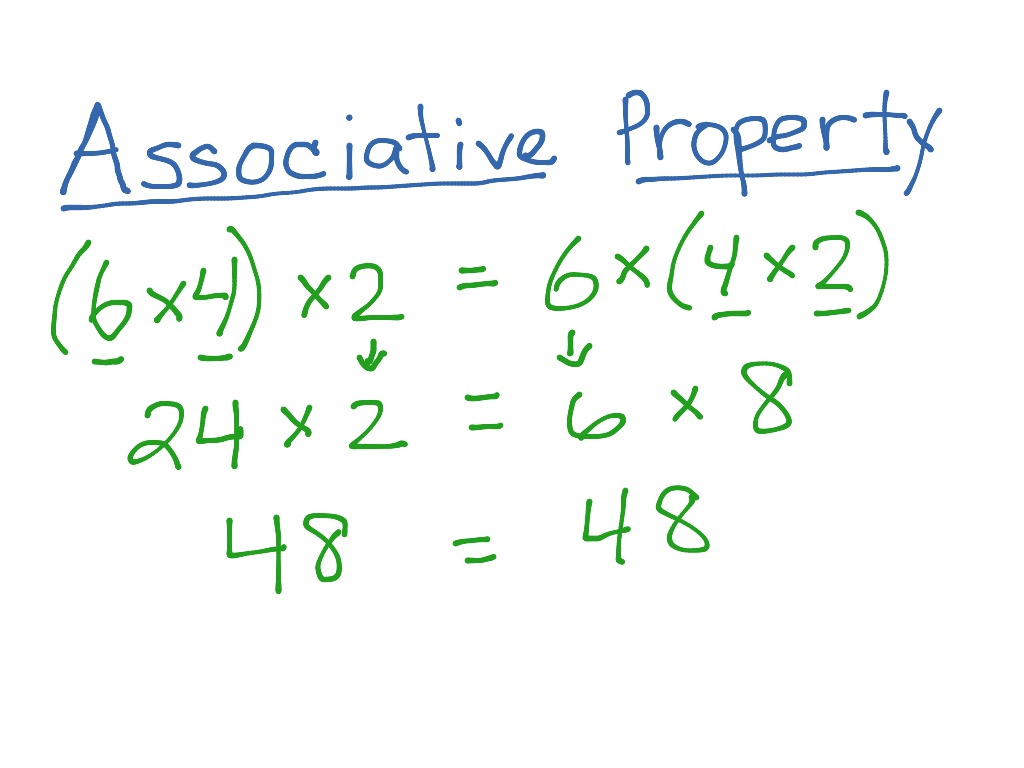
Tips for Mastery
To master the Associative Property of Multiplication, follow these tips:
- Practice, Practice, Practice: Solve a variety of multiplication problems using different grouping strategies to reinforce your understanding.
- Visualize: Draw diagrams or use objects to visualize how grouping numbers differently in multiplication doesn’t change the result.
- Connect with Real-life Scenarios: Look for everyday situations where the associative property comes into play, and try to apply it.
Practice Questions on Associative Property of Multiplication and Addition
Associative Property of Multiplication
- Calculate the following expressions using the associative property of multiplication:
- (3 * 4) * 5
- 3 * (4 * 5)
Are the results the same? Explain why.
- Sarah wants to buy 6 packs of pencils, with each pack containing 8 pencils. How can she use the associative property to calculate the total number of pencils she needs?
- Express 2 * (3 * 4) in its simplified form using the associative property.
- In a garden, there are 5 rows of apple trees, with each row having 7 apple trees. How can you use the associative property to find the total number of apple trees in the garden?
Associative Property of Addition
- Apply the associative property of addition to simplify the following expressions:
- (7 + 9) + 5
- 7 + (9 + 5)
Do both expressions yield the same result? Explain.
- A group of friends went out for dinner, and the bill came to $120. They want to divide it equally among three people. How can they use the associative property of addition to calculate their share?
- Write the expression (15 + 20) + 10 in its simplified form using the associative property of addition.
- If you have three numbers, a, b, and c, how can you apply the associative property of addition to add them together efficiently?

Frequently Asked Questions (FAQs)
What is the difference between the associative property of multiplication and the associative property of addition?
The associative property of multiplication states that you can change the grouping of numbers in a multiplication equation without affecting the result. In contrast, the associative property of addition states that you can change the grouping of numbers in an addition equation without changing the sum. Both properties emphasize how grouping can be altered, but one applies to multiplication, and the other applies to addition.
Why is the associative property important in mathematics?
The associative property is important because it simplifies calculations and makes mathematical operations more efficient. It allows us to rearrange numbers and parentheses in expressions without altering the final result. This property is fundamental in algebra, number theory, and other advanced mathematical fields.
Can you provide more examples of how the associative property is used in real-life situations?
Certainly! Here are a few additional real-life scenarios where the associative property can be applied:
Supermarket Discounts: If you have discounts of 10% on three different items, you can calculate the total discount using the associative property of multiplication.
Travel Expenses: When splitting travel expenses among friends, you can use the associative property of addition to combine various costs efficiently.
Baking Recipes: When adjusting ingredient quantities in a recipe, you can use the associative property of multiplication to scale the recipe up or down.
Feel free to ask more questions or seek further clarification on these concepts!
Conclusion
In this comprehensive guide, we’ve demystified the Associative Property of Multiplication. We’ve explored its definition, and importance, and provided real-life examples to help you grasp the concept. Remember, the associative property is a fundamental tool in mathematics that simplifies calculations and aids in problem-solving. With practice and understanding, you’ll be able to use this property confidently in various mathematical scenarios. Happy multiplying!









